Комментарии преподавателя

Импульс тела. Закон сохранения импульса.

Законы Ньютона позволяют решать различные практически важные задачи, касающиеся взаимодействия и движения тел. Большое число таких задач связано, например, с нахождением ускорения движущегося тела, если известны все действующие на это тело силы. А затем по ускорению определяют и другие величины (мгновенную скорость, перемещение и др.).

Но часто бывает очень сложно определить действующие на тело силы. Поэтому для решения многих задач используют ещё одну важнейшую физическую величину — импульс тела.

• Импульсом тела р называется векторная физическая величина, равная произведению массы тела на его скорость

p = mv.

Импульс — векторная величина. Направление вектора импульса тела всегда совпадает с направлением вектора скорости движения.

За единицу импульса в СИ принимают импульс тела массой 1 кг, движущегося со скоростью 1 м/с. Значит, единицей импульса тела в СИ является 1 кг • м/с.

При расчётах пользуются уравнением для проекций векторов: рх = mvx.

В зависимости от направления вектора скорости по отношению к выбранной оси X проекция вектора импульса может быть как положительной, так и отрицательной.

Слово «импульс» (impulsus) в переводе с латинского означает «толчок». В некоторых книгах вместо термина «импульс» используется термин «количество движения».

Эта величина была введена в науку примерно в тот же период времени, когда Ньютоном были открыты законы, названные впоследствии его именем (т. е. в конце XVII в.).

При взаимодействии тел их импульсы могут изменяться. В этом можно убедиться на простом опыте.

Два шарика одинаковой массы подвешивают на нитяных петлях к укреплённой на кольце штатива деревянной линейке, как показано на рисунке а.

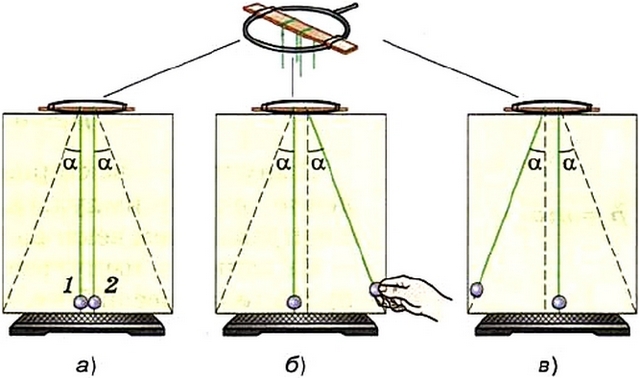
Рис.  Демонстрация закона сохранения импульса

Шарик 2 отклоняют от вертикали на угол а (рис. б) и отпускают. Вернувшись в прежнее положение, он ударяет по шарику 1 и останавливается. При этом шарик 1 приходит в движение и отклоняется на тот же угол а (рис. в).

В данном случае очевидно, что в результате взаимодействия шаров импульс каждого из них изменился: на сколько уменьшился импульс шара 2, на столько же увеличился импульс шара 1.

Если два или несколько тел взаимодействуют только между собой (т. е. не подвергаются воздействию внешних сил), то эти тела образуют замкнутую систему.

Импульс каждого из тел, входящих в замкнутую систему, может меняться в результате их взаимодействия друг с другом. Но

• векторная сумма импульсов тел, составляющих замкнутую систему, не меняется с течением времени при любых движениях и взаимодействиях этих тел

В этом заключается закон сохранения импульса.

Закон сохранения импульса выполняется и в том случае, если на тела системы действуют внешние силы, векторная сумма которых равна нулю. Покажем это, воспользовавшись для вывода закона сохранения импульса вторым и третьим законами Ньютона. Для простоты рассмотрим систему, состоящую только из двух тел — шаров массами m1 и m2, которые движутся прямолинейно навстречу друг другу со скоростями v1 и v2 (рис.).

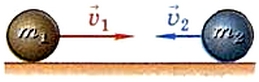
Рис. Система из двух тел — шаров, движущихся прямолинейно навстречу друг другу

Силы тяжести, действующие на каждый из шаров, уравновешиваются силами упругости поверхности, по которой они катятся. Значит, действие этих сил можно не учитывать. Силы сопротивления движению в данном случае малы, поэтому их влияние мы тоже не будем учитывать. Таким образом, можно считать, что шары взаимодействуют только друг с другом.

Из рисунка видно, что через некоторое время шары столкнутся. Во время столкновения, длящегося в течение очень короткого промежутка времени t, возникнут силы взаимодействия F1 и F2, приложенные соответственно к первому и второму шару. В результате действия сил скорости шаров изменятся. Обозначим скорости шаров после соударения буквами v1 и v2.

В соответствии с третьим законом Ньютона силы взаимодействия шаров равны по модулю и направлены в противоположные стороны:

По второму закону Ньютона каждую из этих сил можно заменить произведением массы и ускорения, полученного каждым из шаров при взаимодействии:

m1а1 = -m2а2.

Ускорения, как вы знаете, определяются из равенств:

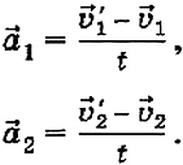
Заменив в уравнении для сил ускорения соответствующими выражениями, получим:

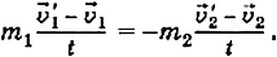
В результате сокращения обеих частей равенства на t получим:

m1(v'1 - v1) = -m2(v'2 - v2).

Сгруппируем члены этого уравнения следующим образом:

m1v1' + m2v2' = m1v1 = m2v2. (1)

Учитывая, что mv = p, запишем уравнение (1) в таком виде:

P'1 + Р'2 = P1 + Р2.(2)

Левые части уравнений (1) и (2) представляют собой суммарный импульс шаров после их взаимодействия, а правые — суммарный импульс до взаимодействия.

Значит, несмотря на то, что импульс каждого из шаров при взаимодействии изменился, векторная сумма их импульсов после взаимодействия осталась такой же, как и до взаимодействия.

Уравнения (1) и (2) являются математической записью закона сохранения импульса.

Поскольку в данном курсе рассматриваются только взаимодействия тел, движущихся вдоль одной прямой, то для записи закона сохранения импульса в скалярной форме достаточно одного уравнения, в которое входят проекции векторных величин на ось X:

m1v'1x + m2v'2х= m1v1x + m2v2x.

 

Домашняя работа.

Задание 1. Ответь на вопросы.

1. Что называют импульсом тела?
2. Что можно сказать о направлениях векторов импульса и скорости движущегося тела?
3. Что означает утверждение о том, что несколько тел образуют замкнутую систему?
4. Сформулируйте закон сохранения импульса.
5. Для замкнутой системы, состоящей из двух тел, запишите закон сохранения импульса в виде уравнения, в которое входили бы массы и скорости этих тел. Поясните, что означает каждый символ в этом уравнении.

Задание 2. Решите задачи.

1. Столкновение автомобилей.

Объясни эти ситуации с точки зрения закона сохранения импульса.

2.Почему большая рыба плывет назад?

Чем отличаются эти ситуации?

3. Для будущих защитников.

При стрельбе существует явление отдачи и на плече у солдата, к которому он прикладывает винтовку, могут появиться синяки. Почему же солдат, держащий на плече базуку ( ручной гранатомет), не испытывает при стрельбе отдачи?

В каком случае ружье стреляет дальше: когда оно неподвижно закреплено, или когда оно подвешено?

 

К занятию прикреплен файл  «Ребусы». Вы можете скачать файл в любое удобное для вас время.

 

Использованные источники: 

http://www.tepka.ru/fizika_9/20.html

http://class-fizika.narod.ru/

Файлы