10 класс. Геометрия. Скрещивающиеся прямые.

Комментарии преподавателя

Скрещивающиеся прямые. Примеры решения задач.  

При решении задач на нахождение угла между скрещивающимися прямыми удобно пользоваться таким алгоритмом:

1. Провести прямую, параллельную одной из двух скрещивающихся прямых так, чтобы она пересекала вторую прямую. Мы получим пересекающиеся прямые, угол между которыми равен углу  между исходными скрещивающимися.

2. Найти треугольник, в котором этот угол будет внутренним углом.

3. С помощью данных задачи найти тригонометрическую функцию этого внутреннего угол или сам угол.

Рассмотрим этот алгоритм подробнее на примере решения задач.

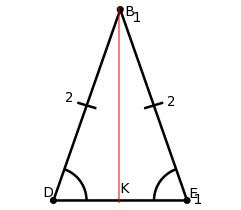
1. В правильной шестиугольной призме 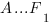, все ребра которой равны 1, найти косинус угла между прямым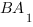и  и :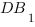

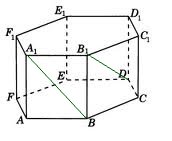Проведем прямую  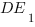параллельно прямой :

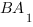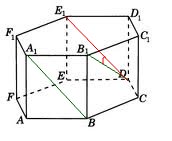
Угол 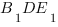 равен углу между прямым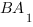и  и 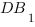, так как эти углы имеют параллельные стороны.

Чтобы найти косинус угла 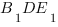, рассмотрим треугольник :

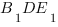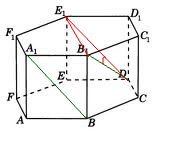Найдем длины сторон этого треугольника. Для этого вспомним, чему равны элементыправильного шестугольника все стороны которого равны 1.

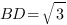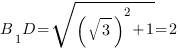,    (из треугольника )

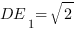 (как диагональ квадрата )

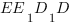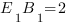 - диаметр окружности, описанной около правильного шестиугольника со сторонами, равными 1.

Мы получили равнобедренный треугольник :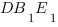

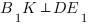
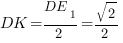
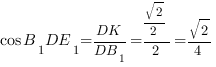
Ответ: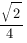 

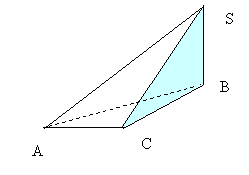
Задача 2. В основании треугольной пирамиды SABC лежит прямоугольный треугольник с прямым углом при вершине С, гипотенузой AB равной 13 и катетом AC, равным 12. Вершина S пирамиды проектируется в точку B основания.     Боковое ребро CS равно 5. Найдите расстояние между ребрами AS и BC.

Решение.

Нам нужно найти расстояние между двумя отрезками AS и BC. Эти отрезки лежат на скрещивающихся прямых. Действительно из условия следует, что точка SABC, а AABC, следовательно, прямая, AS пересекает плоскость ABC и так как BCABC и ABC, то наше утверждение следует из признака скрещивающихся прямых. Теперь мы можем сформулировать задачу точнее: нам нужно найти расстояние между скрещивающимися прямыми.

Определение 1. Расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой, называется расстоянием между скрещивающимися прямыми.(Геометрия 10-11 кл. Л. С. Атанасян и др. М. Просвещенние, 2009 г.)

Следуя этому определению нам необходимо построить плоскость, проходящую через одну из скрещивающих прямых, параллельно другой и построить перпендикуляр к этой плоскости из точки принадлежащей другой прямой.

 Какую прямую выбрать? Обычно такая задача решается перебором.

Мы выбрали прямую AS, проведем через эту прямую плоскость параллельную BC. Для наглядности выполним следующие далеко не очевидные построения.

1. Достроим пирамиду до параллелепипеда. Для этого через точку А в плоскости ABC проведем прямую параллельную прямой ВС и через точку В прямую параллельную прямой АС, точку пепесечения построенных прямых обозначим буквой D. Через точки A, C, D проведем прямые параллельные прямой SB, на каждой из них отложим отрезки равные отрезку BS, и полученные точки соединим отрезками.

2.  Далее построим сечение параллелепипеда ABCDA1B1C1D1 плоскостью ADS, в сечением будет параллелограмм ADSC1  (ребра параллелепипеда AD  и C1S равны и параллельны}

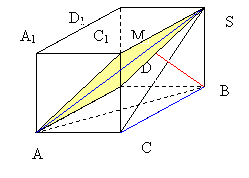3. Плоскости ADS и ADSC1 совпадают или, если хотите, это одна и таже плоскость. Предположим, что это разные не совпадающие плоскости. Тогда по условию эти плоскости имеют три общие точки A, D и S. Но тогда согласно аксиоме "Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей" точки A, D и S лежат на одной прямой, тогда SАD, так как  АD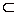АВС, то SАВС, но это противоречит условию. Значит наше предположение не верно.  Тогда плоскости ADS  и ADSC1совпадают.

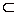 4. Пусть прямая BM перпендикулярна прямой DS. Отрезок BM есть кратчайшее расстояние между скрещивающимися прямыми.  Докажем это утверждение. Из условия следует, что BC  BS и BCAC, так как AC||DB, то BCDB, так как к тому же BD и BS пересекающиеся прямые, то BCDBS, но тогда и ADDBS,  посколько  BMDBS, то BMAD. Так как BM перпендикулярна к двум пересекающимся прямым AD и DS лежащим в плоскости ADSC1, то BMADSC1.

5. Для того чтобы вычислить длину отрезка BM нам необходимо вычислить длины отрезков BC, BS и DS.

По условию C прямой, поэтому ABC  - прямоугольный, следовательно, AB2= AC2  + BC2;

BC2 = 132 - 122;

BC = 5;

По условию S проектируется в B, поэтому BSABC, BC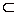ABC, следовательно BSBC. значит CSB  - прямоугольный, следовательно, CS2 = BC2 + BS2;

BS2 = (5)2 - 52;

BS = 10;

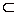BSABC, по построению BDABC, поэтому BSBD откуда следует, что BDM  - прямоугольный, следовательно, DM2 = DB2 - BM 2;

BMS прямоугольный, следовательно,  MS2 = BS2 - BM2

Пусть BM = x, тогда

DM = ;

 MS =   ;

Так как BM общий катет двух прямоугольных треугольников с гипотенузами 10 и 12, то 0 < x < 10 и поэтому 102 - x2 > 0, 122 - x2 > 0 .

Составить уравнение можно двумя способами либо использовать очевидное равенство DS = DM + MS, либо исплльзовать свойство перпендикуляра проведенного из вершины прямого угла к гипотенузе. И в том и другом случае получим иррациональное уравнение. Эти уравнения имеют  разную сложность. Пойдем по второму пути, так как , по нашему мнению, уравнение будеть более простым.

BM2 = DMMS;

x2 =  ;  возведем обе части уравнения в квадрат, учитывая выше изложенные рассуждения, получим уравнение равносильное данному.

x4 = 14400 - 100x2 - 144x2  +  x4;

244x2 = 14400;

x = .

Растояние между ребрами AS и BC равно .

Решить эту задачу можно и иначе. В учебнике Геометрия 7-11кл. А. В. Погорелов М. Просвещение 2009г. понятие расстояние между скрещивающими прямыми определяется так.

Определение 2. Расстоянием между скрещивающимися прямыми называют длину общего перпендикуляра к этим прямым.

Чтобы построить  общий перпендикуляр скрещивающих прямых выполним следующие построения. Чтобы не повторятся строить параллелепипед мы не будем и рисунок будет проще....

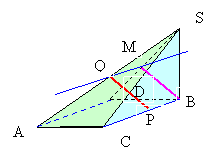Через точку А в плоскости АВС проведем AD||BC и через точку В проведем BD||AC. В плоскости SDB из точки В проведем BMDS и через точку М проведем QM||AD. Через точку Q проведем QP||MB. Отрезок QP - это общий перпендикуляр скрещивающихся прямых AS и BC.

Выше мы доказали, что BMADS. Так как по построениюQP||BM, то  QPADS.  AD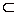ADS поэтому  QPAD.

С другой стороны BC перпендикулярна двум пересекающимся прямым BS и BD, следовательно, BM BC, но тогда так как MB||QP, то  QPBC.

QMBP - параллелограмм, следовательно, QP = BM. Как вычисляется длина отрезка  BM. мы рассотрели выше.

Задача 3. В основании пирамиды SABCD лежит прямоугольник.
BC = a, DC = b.
Основание высоты пирамиды совпадает с центром симметрии ABCD.
Боковое ребро пирамиды равно c.
Найти растояние между ребрами AD и SC.

Решение.

   Ребра    AD и SC лежат на скрещивающихся прямых. Прямая AD параллельна плоскости SBC, проходящей через прямую SC. Проведем в этой плоскости SEBC.  и через точку E проведем прямую ОE, где О основание высоты пирамиды. Точку пересения прямых ОЕ и AD обозначим Р.  В плоскости SPE проведем PMSE. Отрезок PM это кратчайшее расстояние между скрещивающими прямыми AD и SC. Докажем это утверждение.  По построению ОЕ проекция наклонной SE через основание, которой проведена прямая ВС. Из теоремы о трех перпендикулярах следует, что  PЕВС. Прямые  SE и PE лежат в плоскости SEP и S пересекающиеся, следовательно, BCSEP откуда следует, РМВС. Таким образом РМ перпендикулярна двум пересекающимся прямым  SE и BC лежащим в плоскости SВС, значит по признаку перпендикулярности прямой к плоскости РМ SВС и согласно определению 1 является растоянием между скрещивающимися прямыии AD  и SC.

Теперь вычислим PM. По условию основание высоты пирамиды совпадает с центром симметрии прямоугольника, поэтому O середина диагоналей AC и BD, тогда, во первых  OPE, во вторых боковые ребра SA = SB = SC = SD.  Из равенства боковых ребер пирамиды следует, что  SBC равнобедренный треугольник и поэтому его высота SE является медианой и поэтому EC = 0,5a и SE2= c2 - 0,25a2.

Из прямоугольного треугольника SOE следует, что SO2 = SE2 - OE2 ,

SO2 = c2 - 0,25a2 - 0,25b2 .

 Из этого же треугольника  и определения синуса для острого угла следует, что

 sinSEO=.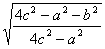

Из прямоугольного треугольника PME и определения синуса для острого угла следует, что  PM = PEsinSEO, тогда

PM=b.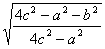

Обратите внимание на то, что искомый отрезок находится в плоскости перпендикулярной к одной из скрещивающихся прямых. Этот факт позволяет нам предложить следущий способ решения задач на нахождение расстояния между скрещивающимися прямыми.

1. Строим плоскость перпендикулярную к одной из скрещивающихся прямых. В задаче 1 это плоскость DD1SC.

2. Проецируем каждую из скрещивающихся прямых на эту плоскость. Проекцией одной из них будет точка. В задаче 1 проекция прямой ВС будет точка С, а проекция прямой AS будет прямая SD. Таким образом да И данную задачу формулируем так: "найти расстояние от точки до прямой. В задаче 1 найти расстояние от точки С до прямой  DS.

3. Проводим перпендикуляр от точки до прямой. Это будет всегда перпендикуляр, проведенный из вершины прямого угла прямоугольного треугольника  к гипотенузе и, следовательно, всегда можно применить его свойство, для чего прдварительно находим гипотенузу и катеты прямоугольного треугольника..

Для закрепления навыка нахождения расстояния между скрещивающимися проямыми предлагаем решить следующие задачи. Постройте изображение куба и найдите пары скрещивающиеся прямых. Для каждой выбранной пары  прямых докажите, используя признак скрещивающихся прямых, что это скрещивающиеся прямые.

Замечание. В том случае, когда возникают затруднения в нахождении пар скрещивающихся прямых  можно самостоятельно изготовить из бумаги или из спичек и пластелина модель куба и на этой модели выполнять поиск прямых. Желательно модель размещать в различных положениях. После работы с моделью проделайте эту работу мысленно, пытаясь в воображении представить модель куба и лишь потом перейти к рисунку.

Задача 4. 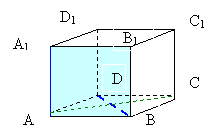 Дан куб ABCDA1B1C1D1.
AB = 5 см.
Найти расстояние между прямыми AA1 и BD.
Подсказка. Обратите внимание на отрезок АC

ИСТОЧНИК

http://ege-ok.ru/2012/03/26/ugol-mezhdu-skreshhivayushhimisya-pryamyimi-zadanie-s2

http://dok.opredelim.com/docs/index-14359.html

http://viripit.ru/Page8.htm

http://www.youtube.com/watch?v=esy12BGkdlA

http://www.youtube.com/watch?v=J2vh5DyWmrQ

http://www.youtube.com/watch?v=ojUGjoLbBH0

http://www.otbet.ru/book/class-10/geometria/uchebnik-glazkov-yu-a-testy-po-geometrii/

Файлы