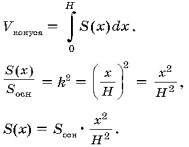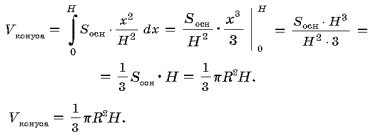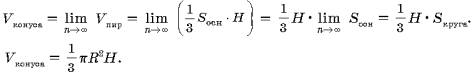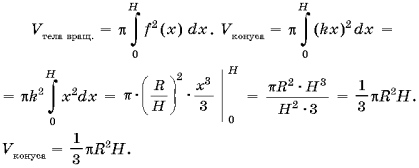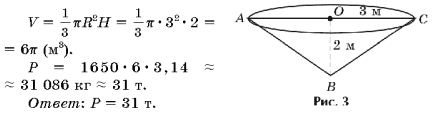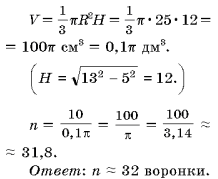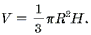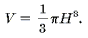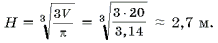11 класс. Геометрия. Объемы тел.

Комментарии преподавателя

Объем конуса

 1.  Историческая справка

Конус в переводе с греческого «konos» означает «сосновая шишка». С конусом люди знакомы с глубокой древности. В 1906 году была обнаружена книга Архимеда (287–212 гг. до н. э.) «О методе», в которой дается решение задачи об объеме общей части пересекающихся цилиндров. Архимед приписывает честь открытия этого принципа Демокриту (470–380 гг. до н. э.) – древнегреческому философу-материалисту. С помощью этого принципа Демокрит получил формулы для вычисления объема пирамиды и конуса.

Много сделала для геометрии школа Платона (428–348 гг. до н. э.). Платон был учеником Сократа (470–399 гг. до н. э.). Он в 387 г. до н. э. основал в Афинах Академию, в которой работал 20 лет. Каждый, входящий в Академию, читал надпись: «Пусть сюда не входит никто, не знающий геометрии». Школе Платона, в частности, принадлежит: а) исследование свойств призмы, пирамиды, цилиндра и конуса; б) изучение конических сечений.

Большой трактат о конических сечениях был написан Аполлонием Пергским (260–170 гг. до н. э.) – учеником Евклида (III в. до н. э.), который создал великий труд из 15 книг под названием «Начала». Эти книги издаются и по сей день, а в школах Англии по ним учатся до сих пор.

2. Объяснение нового материала

Объем конуса

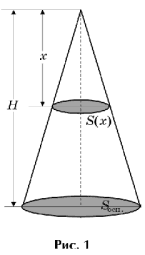
1-е доказательство (рис. 1).

2-е доказательство.

За величину объема конуса принимается предел, к которому стремится объем правильной пирамиды, вписанной в конус, при неограниченном удвоении числа сторон ее основания.

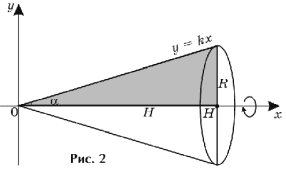
3-е доказательство (рис. 2).

3.  Решение задач на объем конуса

Задача 1. Авиационная бомба среднего калибра дает при взрыве воронку диаметром 6 м и глубиной 2 м. Какое количество земли (по массе) выбрасывает эта бомба, если 1 м3 земли имеет массу 1650 кг?

Решение (рис. 3).

Задача 2. Высветить слайд «Сбор смолы с сосен».

Дано:

коническая воронка
D = 10 см
L = 13 см
V – ?

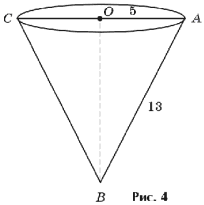
Смолу для промышленных нужд собирают, подвешивая конические воронки к соснам. Сколько воронок диаметром 10 см с образующей 13 см нужно собрать, чтобы заполнить 10-литровое ведро?

Решение (рис. 4).

Задача 3. Прослушаем фонограмму старинной легенды восточных народов, рассказанной А.С. Пушкиным в «Скупом рыцаре».

«... Читал я где-то,
Что царь однажды воинам своим
Велел снести земли по горсти в кучу.
И гордый холм возвысился,
И царь мог с высоты с весельем озирать
И дол, покрытый белыми шатрами,
И море, где бежали корабли.»

Это одна из немногих легенд, в которой при кажущемся правдоподобии нет и зерна правды. Докажите геометрически, что если бы какой-нибудь древний деспот вздумал осуществить такую затею, он был бы обескуражен мизерностью результата. Перед ним высилась бы настолько жалкая куча земли, что никакая фантазия не смогла бы раздуть ее в легендарный «гордый холм».

Войско в 100 000 воинов считалось очень внушительным.

V = 0,2ж100 000 = 20 000 дм3 = 20 м3.

Угол откоса Ј 45°, иначе земля начнет осыпаться. Возьмем угол откоса наибольшим возможным, т. е. 45° (рис. 5).

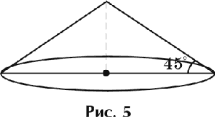
Итак,

дано:

конус
V = 20 м3 
a = 45° 
Найти: H конуса

Решение.

Так как H = R, то

Надо обладать очень богатым воображением, чтобы земляную кучу в 2,7 м (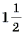 человеческих роста) назвать «гордым холмом». Сделав расчет для меньшего угла, мы получили бы еще более скромный результат.

У Аттилы было самое многочисленное войско, которое знал древний мир. Историки оценивают его в 700 000 человек. К сведению, Аттила – предводитель гуннов, кочевого народа, сложившегося в Приуралье из многих племен. Массовое передвижение гуннов на запад (с 70-х гг. IV в.) дало толчок «великому переселению народов». Наибольшего могущества гуннская держава достигла при Аттиле (?–453 гг.), который возглавил опустошительные походы в Восточно-Римскую империю (413 г., 447 г., 448 г., 451 г.). Но в 451 году на Каталаунских полях (равнина в северо-восточной Франции к западу от города Труа) войска Западно-Римской империи в союзе с франками, вест-готами, бургундами, аланами и др. разгромили гуннов во главе с Аттилой, что привело к распаду гуннской державы.

Если бы все воины Аттилы участвовали в насыпании холма, образовалась бы куча повыше вычисленной нами, но не очень. Советую вам самим дома вычислить высоту кургана и подумать, удовлетворила бы такая высота честолюбие Аттилы или нет.

ИСТОЧНИК

http://mat.1september.ru/2000/no42_1.htm

http://make-me-smart.com/geometry/polyhedron2

http://www.youtube.com/watch?v=ZzwuQfnqkwg

http://www.youtube.com/watch?v=mr4lruf3VV4

http://www.youtube.com/watch?v=Ai3DO-Ppr54

http://v.900igr.net/zip/a0a850ced5fbc2f4822cf7e5ddfd2f08.zip

http://nsportal.ru/sites/default/files/2013/04/13/obem_konusa_otkrytyy_urok_2012.docx

http://www.resolventa.ru/uslugi/uslugi12.htm

http://2mb.ru/matematika/geometriya/obem-piramidy/#ixzz4RTfQykvU

Файлы