Простые механизмы. Рычаги. Момент силы. Физика. 7 класс.

Комментарии преподавателя

ПРОСТЫЕ МЕХАНИЗМЫ

БЛОК

В современной технике для переноса грузов на стройках и предприятиях широко используются грузоподъемные механизмы, незаменимыми составными частями которых можно назвать простые механизмы. Среди них древнейшие изобретения человечества: блок и рычаг. Древнегреческий ученый Архимед облегчил труд человека, дав ему при использовании своего изобретения выигрыш в силе, и научил менять направление действия силы.

Блок - это колесо с желобом по окружности для каната или цепи, ось которого жестко прикреплена к стене или потолочной балке. Грузоподъемные устройства обычно используют не один, а несколько блоков. Система блоков и тросов, предназначенная для повышения грузоподъемности, называется полиспаст.

Подвижный и неподвижный блок - такие же древнейшие простые механизмы, как и рычаг. Уже в 212 г.до н.эры с помощью крюков и захватов, соединенных с блоками, сиракузцы захватывали у римлян средства осады. Сооружением военных машин и обороной города руководил Архимед.

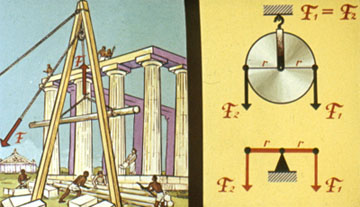
Неподвижный блок Архимед рассматривал как равноплечий рычаг.
Момент силы, действующей с одной стороны блока, равен моменту силы, приложенной с другой стороны блока. Одинаковы и силы, создающие эти моменты.
Выигрыш в силе при этом отсутствует, но такой блок позволяет изменить направление действия силы, что иногда необходимо.

Подвижный блок Архимед принимал за неравноплечий рычаг, дающий выигрыш в силе в 2 раза. Относительно центра вращения действуют моменты сил, которые при равновесии должны быть равны.
Архимед изучил механические свойства подвижного блока и применил его на практике. По свидетельству Афинея, "для спуска на воду исполинского корабля, построенного сиракузским тираном Гиероном, придумывали много способов, но механик Архимед, применив простые механизмы, один сумел сдвинуть корабль с помощью немногих людей. Архимед придумал блок и посредством него спустил на воду громадный корабль".

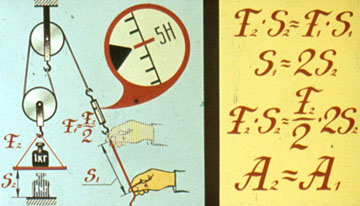
Блок не дает выигрыша в работе, подтверждая "золотое правило" механики. В этом легко убедиться, обратив внимание на расстояния, пройденные рукой и гирей.

Спортивные парусные суда, как и парусники прошлого, не могут обойтись без блоков при постановке парусов и управлении ими. Современным судам нужны блоки для подъема сигналов, шлюпок.

Эта комбинация подвижных и неподвижных блоков на линии электрофицированной железной дороги для регулировки натяжения проводов.

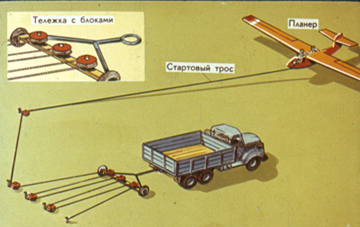
Такой системой блоков могут пользоваться планеристы для подъема в воздух своих аппаратов.

ВОРОТ

Это два колеса, соединенные вместе и вращающиеся вокруг одной оси, например, колодезный ворот с ручкой.

Такое сложное громоздкое устройство средневекового периода - ворот или ступальные колеса широко использовались в рудничном деле. Их приводили в движение люди, ступая по планкам колеса.

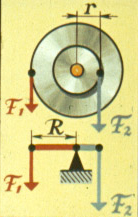
Ворот можно рассматривать как неравноплечий рычаг: выигрыш в силе, даваемый им, зависит от соотношения радиусов R и r.

ЛЕБЁДКА

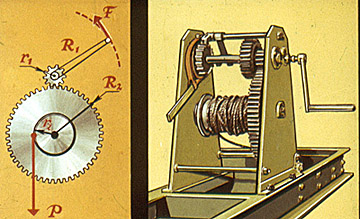
Лебедка - конструкция , состоящая из двух воротов с промежуточными передачами в механизме привода.

Грузоподъемность современных лебедок может быть свыше 100 кН. Они работают на канатных дорогах, на буровых установках, выполняют строительно-монтажные и погрузочно-разгрузочные работы.

Лебедка с двигателем внутреннего сгорания.

Электрическая передвижная лебедка.

ЗУБЧАТАЯ ПЕРЕДАЧА

- система находящихся в зацеплении зубчатых колес ( шестеренок) в какой-то мере аналогична вороту.

НАКЛОННАЯ ПЛОСКОСТЬ

Наклонная плоскость применяется для перемещения тяжелых предметов на более высокий уровень без их непосредственного поднятия.
К таким устройствам относятся пандусы, эскалаторы, обычные лестницы и конвейеры.
Если нужно поднять груз на высоту, всегда легче воспользоваться пологим подъемом, чем крутым. Причем, чем положе уклон, тем легче выполнить эту работу. Когда время и расстояние не имеют большого значения , а важно поднять груз с наименьшим усилием, наклонная плоскость оказывается незаменима.

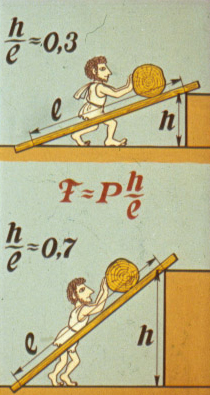
С помощью этих рисунков можно объяснить, как работает простой механизм НАКЛОННАЯ ПЛОСКОСТЬ.
Классические расчеты действия наклонной плоскости и других простых механизмов принадлежат выдающемуся античному механику Архимеду из Сиракуз.

При строительстве храмов египтяне транспортировали, поднимали и устанавливали колоссальные обелиски и статуи, вес которых составлял десятки и сотни тонн! Все это можно было сделать, используя среди других простых механизмов наклонную плоскость.
Главным подъемным приспособлением египтян была наклонная плоскость - рампа. Остов рампы, то есть ее боковые стороны и перегородки, на небольшом расстоянии друг от друга пересекавшие рампу, строились из кирпича; пустоты заполнялись тростником и ветвями. По мере роста пирамиды рампа надстраивалась. По этим рампам камни тащили на салазках таким же образом, как и по земле, помогая себе при этом рычагами. Угол наклона рампы был очень незначительным - 5 или 6 градусов.

Колонны древнего египетского храма в Фивах.

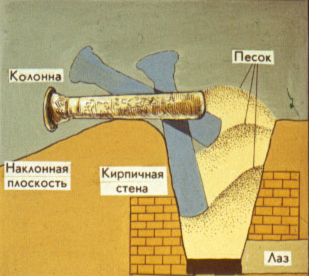
Каждую из этих огромных колонн рабы втаскивали по рампе- наклонной плоскости. Когда колонна вползала в яму, через лаз выгребали песок, а затем разбирали кирпичную стенку и убирали насыпь. Таким образом, например, наклонная дорога к пирамиде Хафра при высоте подъема в 46 метров имела длину около полукилометра.

"Тело на наклонной плоскости удерживается силой, которая ... по величине во столько раз меньше веса этого тела, во сколько раз длина наклонной плоскости больше ее высоты".
Это условие равновесия сил на наклонной плоскости сформулировал голландский ученый Симон Стевин (1548-1620).

Рисунок на титульном листе книги С. Стевина, которым он подтверждает свою формулировку.

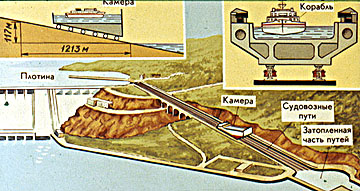
Очень остроумно использована наклонная плоскость на Красноярской ГЭС. Здесь вместо шлюзов действует судовозная камера, движущаяся по наклонной эстакаде. Для ее передвижения необходимо тяговое усилие в 4000 кН.

А почему горные дороги вьются пологим "серпантином"?

КЛИН

Клин - одна из разновидностей простого механизма под названием "наклонная плоскость". Клин состоит из двух наклонных плоскостей, основания которых соприкасаются. Его применяют, чтобы получить выигрыш в силе, то есть при помощи меньшей силы противодействовать большей силе.
При рубке дров, чтобы облегчить работу, в трещину полена вставляют металлический клин и бьют по нему обухом топора.
Идеальный выигрыш в силе, даваемый клином, равен отношению его длины к толщине на тупом конце .Из-за большого трения его КПД столь мал, что идеальный выигрыш не имеет особого значения.

ВИНТ

Другой разновидностью наклонной плоскости является винт.
Винт - наклонная плоскость, навитая на ось. Резьба винта – это наклонная плоскость, многократно обернутая вокруг цилиндра. Идеальный выигрыш в силе, даваемый клином, равен отношению его длины к толщине на тупом конце. Реальный выигрыш клина определить трудно.
Из-за большого трения его КПД столь мал, что идеальный выигрыш не имеет особого значения. В зависимости от направления подъема наклонной плоскости винтовая резьба может быть левой или правой.
Примеры простых устройств с винтовой резьбой – домкрат, болт с гайкой, микрометр, тиски.

Момент силы.

Условием равновесия рычага F1/F2 = l2/l1 можно пользоваться, если к рычагу приложены только две силы.

А каково условие равновесия рычага в случае, когда к рычагу приложено несколько сил?

Чтобы найти это условие, перепишем равенство F1/F2 = l2/l1 в виде F1l1 = F2l2. Теперь величины, характеризующие силу, стремящуюся вращать рычаг в одном направлении, находятся в одной части равенства, а величины, характеризующие силу, стремящуюся вращать рычаг в противоположном направлении, — в другой части равенства.

Произведение модуля силы на ее плечо называют моментом силы: М = FI. Момент первой силы M1 = F1l1 а момент второй силы М2 = F2l2. Поэтому условие F1l1 = F2l2 можно переписать теперь в виде М1 = М2.

С использованием понятия момента силы условие равновесия рычага можно сформулировать так: рычаг находится в равновесии, если момент силы, стремящейся вращать рычаг в одном направлении, равен моменту силы, стремящейся вращать его в противоположном направлении.

Опыт и расчет показывают, что это справедливо и тогда, когда к рычагу приложено несколько сил: рычаг находится в равновесии, если сумма моментов сил, стремящихся вращать рычаг в одном направлении, равна сумме моментов сил, стремящихся вращать его в противоположном направлении.

Условие равновесия рычага в таком виде называют правилом моментов. Приведем пример использования этого правила.

Решим задачу

Какой массы груз надо подвесить в точке А (рис. 25.5, а), чтобы рычаг находился в равновесии? Масса каждого груза равна 100 г, расстояние между соседними штрихами на рычаге равно 10 см.

Рис. 25.5. К решению задачи

Ответ: 0,4 кг.

Домашнее задание

Задание 1. Ответь на вопросы.

1. Что такое рычаг? Приведите примеры рычага.
2. Что такое плечо силы?
3. Сформулируйте условие равновесия рычага.
4. Как с помощью рычага получить выигрыш в пути? Приведите примеры такого использования рычага.
5. Что такое момент силы? Сформулируйте правило моментов.

Задание 2. Реши ребус.

К занятию прикреплен файл  «Это интересно!». Вы можете скачать файл в любое удобное для вас время.

Использованные источники: http://www.tepka.ru/fizika_7  , http://class-fizika.narod.ru
 

 

 

Файлы