Понятие функции. Способы задания функции

Функцией называется закон, по которому числу х из заданного множества Х, поставлено в соответствие только одно число у, пишут 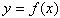, при этом x называют аргументом функции, y называют значением функции.

Существуют разные способы задания функций.

1. Аналитический способ.

Аналитический способ - это наиболее часто встречающийся способ задания функции.

Заключается он в том, что функция задается формулой, устанавливающей, какие операции нужно произвести над х, чтобы найти у. Например .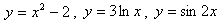

Рассмотрим первый пример - 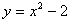. Здесь значению x = 1 соответствует 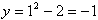, значению x = 3 соответствует 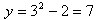и т. д.

Функция может быть задана на разных частях множества X разными функциями.

Например:

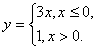
Во всех ранее приведенных примерах аналитического способа задания, функция была задана явно. То есть, справа стояла переменная y, а слева формула от переменной х. Однако, при аналитическом способе задания, функция может быть задана и неявно.

Например 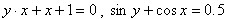. Здесь, если мы задаем переменной x значение, то, чтобы найти значение переменной у (значение функции), мы должны решить уравнение. Например, для первой заданной функции при х = 3, будем решать уравнение:

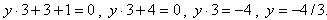. То есть, значение функции при х = 3 равно -4/3.

При аналитическом способе задания, функция может быть задана параметрически - это, когда х и у выражены через некоторый параметр t. Например,

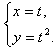
Здесь при t = 2, x = 2, y = 4. То есть, значение функции при х = 2 равно 4.

2. Графический способ.

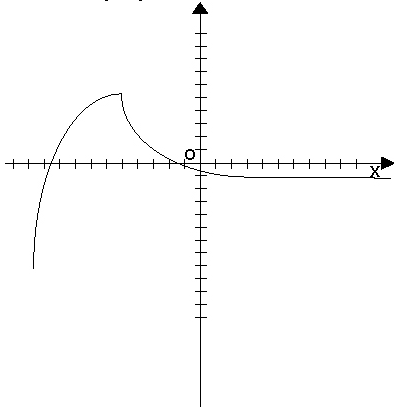
При графическом способе вводится прямоугольная система координат и в этой системе координат изображается множество точек с координатами (x,y). При этом 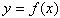. Пример:

3. Словесный способ.

Функция задается с помощью словесной формулировки. Классический пример – функция Дирихле.

«Функция равна 1, если х – рациональное число; функция равна 0, если х – иррациональное число».

4. Табличный способ.

Табличный способ наиболее удобен, когда множество Х конечно. При этом способе составляется таблица, в которой каждому элементу из множества Х, ставится в соответствие число Y.

Пример:

Табличный способ задания функции очень удобен при обработке результатов исследований. Например, при выявлении зависимости между уровнем загрязнения окружающей среды и количеству людей, заболевших раком.