9 класс. Алгебра. Определение числовой функции. Способы задания функций.

Комментарии преподавателя

Область определения функции с корнем

Функция с квадратным корнем 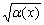 определена только при тех значениях «икс», когдаподкоренное выражение неотрицательно: 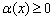. Если корень расположился в знаменателе 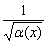, то условие очевидным образом ужесточается: . 

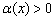Пример 5

Найти область определения функции 

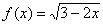
Решение: подкоренное выражение должно быть неотрицательным:

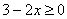
Прежде чем продолжить решение, напомню основные правила работы с  неравенствами, известные ещё со школы.

 Итак, для неравенства равносильны следующие преобразования:

1) Слагаемые можно переносить из части в часть со сменой знака.

2) Обе части неравенства можно умножить на положительное число.

3) Если обе части неравенства умножить на отрицательное число, то необходимо сменитьзнак самого неравенства. Например, если было «больше», то станет «меньше»; если было «меньше либо равно», то станет «больше либо равно».

В неравенстве 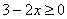 перенесём «тройку» в правую часть со сменой знака (правило №1):

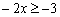
Умножим обе части неравенства на –1 (правило №3):

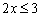
Умножим обе части неравенства на 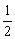 (правило №2):

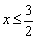
Ответ: область определения: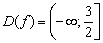 

Ответ также можно записать эквивалентной фразой: «функция определена при ».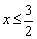
Геометрически область определения изображается штриховкой соответствующих интервалов на оси абсцисс. В данном случае:

Ещё раз напоминаю геометрический смысл области определения – график функции 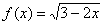 существует только на заштрихованном участке и отсутствует при .

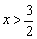В большинстве случаев годится чисто аналитическое нахождение области определения, но когда функция сложная, следует чертить ось 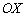 и делать пометки.

Пример 6

Найти область определения функции 

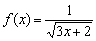
Это пример для самостоятельного решения.

Когда под квадратным корнем находится квадратный двучлен или трёхчлен, ситуация немного усложняется, и сейчас мы подробно разберём технику решения:

Пример 7

Найти область определения функции 

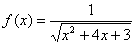
Решение: подкоренное выражение должно быть строго положительным, то есть нам необходимо решить неравенство 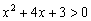. На первом шаге пытаемся разложить квадратный трёхчлен на множители:

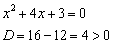
Дискриминант положителен, ищем корни:

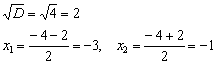
Таким образом, парабола 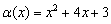 пересекает ось абсцисс в двух точках, а это значит, что часть параболы расположена ниже оси (неравенство 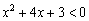), а часть параболы – выше оси (нужное нам неравенство ).

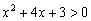Поскольку коэффициент 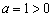, то ветви параболы смотрят вверх. Из вышесказанного следует, что на интервалах  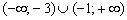выполнено неравенство  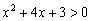(ветки параболы уходят вверх на бесконечность), а вершина параболы расположена на промежутке  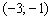ниже оси абсцисс, что соответствует неравенству :

 

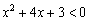Обратите внимание, что сами точки 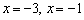 выколоты (не входят в решение), поскольку неравенство у нас строгое.

Ответ: область определения: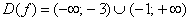 

Вообще, многие неравенства (в том числе рассмотренное) решаются универсальнымметодом интервалов, известным опять же из школьной программы. Но в случаях квадратных дву- и трёхчленов, на мой взгляд, гораздо удобнее и быстрее проанализировать расположение параболы относительно оси .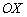 

Источник конспекта: http://www.mathprofi.ru/oblast_opredeleniya.html

Источник видео: http://www.youtube.com/watch?v=6aqZHIHeMeQ

Файлы

Нет дополнительных материалов для этого занятия.