11 класс. Математика. Подготовка к ЕГЭ. Преобразование тригонометрических выражений. Тригонометрические функции суммы и разности аргументов.
11 класс. Математика. Подготовка к ЕГЭ. Преобразование тригонометрических выражений. Тригонометрические функции суммы и разности аргументов.
Комментарии преподавателя
Тангенс суммы и разности аргументов
В этом параграфе речь пойдет о том, как тангенс суммы или разности аргументов выражается через тангенсы аргументов. Соответствующие формулы выглядят следующим образом:
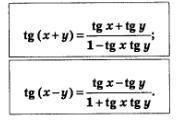
При этом, разумеется, предполагается, что все тангенсы имеют смысл, т.е. что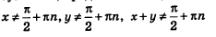 (для первой формулы),
(для первой формулы),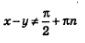 (для второй формулы).
(для второй формулы).
Доказательства этих формул достаточно сложны, мы приведем одно из них в конце параграфа. Но сначала рассмотрим ряд примеров, показывающих, как используются эти формулы на практике.
Пример 1. Вычислить: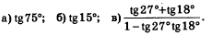
Решение, а) Воспользуемся тем, что 75° = 45° + 30°. Получим:
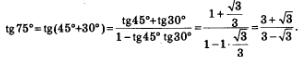
Есть смысл избавиться от иррациональности в знаменателе, домножив и числитель, и знаменатель полученной дроби на
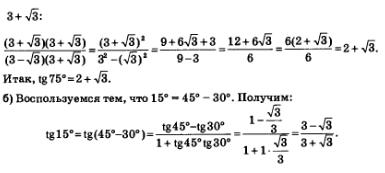
Есть смысл избавиться от иррациональности в знаменателе, домножив и числитель, и знаменатель полученной дроби на
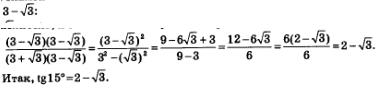
в) Заметим, что заданное выражение представляет собой правую часть формулы «тангенс суммы» для аргументов 27° и 18°. Значит,
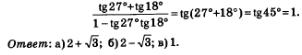
Пример 2. Доказать тождество: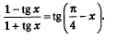
Решение. Применим к правой части проверяемого тождества формулу «тангенс разности». Имеем:
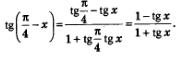
Замечание. Когда речь идет о доказательстве тригонометрического тождества или о преобразовании тригонометрического выражения, всегда предполагается, что аргументы принимают только допустимые значения. Так, в рассмотренном примере доказанное тождество справедливо при условии, что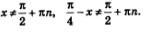
Пример 3. Вычислить
Решение. Воспользуемся тождеством, полученным в предыдущем примере:

Если мы вычислим tg х, то вычислим и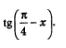
Значение соs x; задано, значение tg х найдем с помощью соотношения

По условию аргумент x принадлежит второй четверти, а в ней тангенс отрицателен. Поэтому из равенства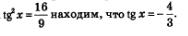
Подставим найденное значение в правую часть формулы (1):
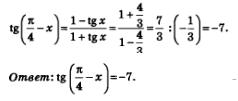
В заключение докажем, как было обещано, формулу тангенса суммы. Кроме того, приведем довольно любопытный пример, показывающий неожиданное применение формулы тангенса суммы.
Имеем:
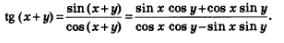
Разделим в полученной дроби и числитель, и знаменатель почленно на соs х соз у. Получим:
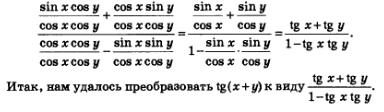
Пример 4. Доказать, что 1° — иррациональное число.
Решение. Предположим противное, что tg 1°— рациональное число :tg 1 °=r, где г — рациональное число. Имеем:
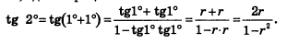
Получилось рациональное число, обозначим его q; итак tg 2°=q.
Рассуждая аналогично, устанавливаем, что: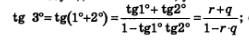 снова получили рациональное число. Продолжая процесс, получим, что 4°, 5°, 60° — рациональные числа. Но
снова получили рациональное число. Продолжая процесс, получим, что 4°, 5°, 60° — рациональные числа. Но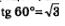 а это — иррациональное число. Получили противоречие, значит, сделанное предположение неверно, т.е. tg 1° — иррациональное число.
а это — иррациональное число. Получили противоречие, значит, сделанное предположение неверно, т.е. tg 1° — иррациональное число.
ИСТОЧНИК
http://school.xvatit.com/index.php?title=Тангенс_суммы_и_разности_аргументов
http://www.youtube.com/watch?v=qSdc5MkOEpk
http://www.youtube.com/watch?v=j195TUfksAY
http://11book.ru/images/shcoolbook_ru/10/10_a_mord_baz.pdf
http://chaulitasjo.science/pic-zadacha.uanet.biz/uploads/61/76/6176c60983745d17f71a3337ee5c8100/%D0%9C%D0%B5%D1%80%D0%B7%D0%BB%D1%8F%D0%BA-%D0%90.%D0%93.-%D0%9F%D0%BE%D0%BB%D0%BE%D0%BD%D1%81%D0%BA%D0%B8%D0%B9-%D0%92.%D0%91.-%D0%A0%D0%B0%D0%B1%D0%B8%D0%BD%D0%BE%D0%B2%D0%B8%D1%87-%D0%95.%D0%9C.-%D0%AF%D0%BA%D0%B8%D1%80-%D0%9C.%D0%A1.-%D0%A2%D1%80%D0%B8%D0%B3%D0%BE%D0%BD%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%8F.-%D0%97%D0%B0%D0%B4%D0%B0%D1%87%D0%BD%D0%B8%D0%BA-%D0%BA-%D1%88%D0%BA%D0%BE%D0%BB%D1%8C%D0%BD%D0%BE%D0%BC%D1%83-%D0%BA%D1%83%D1%80%D1%81%D1%83.-8-11-%D0%BA%D0%BB%D0%B0%D1%81%D1%81-1998.jpg
http://cdndl.zaycev.net/117190/12852/didyulya_-_put_domoy_(zaycev.net).mp3
http://nsportal.ru/sites/default/files/2011/12/28/urok_po_trigonometrii.pptx
http://v.5klass.net/zip/a78a0686cc07a7f0ba76cd8044d235a6.zip
http://internika.org/sites/default/files/imagecache/work_n/users/user16424/prezentaciya1.jpg
http://prilogenie-blank-0155487.ru/wp-content/uploads/2015/09/16-09-2015-10-32-54-c5636218772c57bc34c5ed8cca852b57.jpg
Файлы
Нет дополнительных материалов для этого занятия.
