Статистика. Статистическое наблюдение.

Комментарии преподавателя

Средние величины в статистике: сущность, свойства, виды. 

Наиболее распространенной формой статистических показателей, используемой в экономических исследованиях, является средняя величина, представляющая собой обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени.

Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности, ведь значения признака отдельных единиц совокупности колеблются в ту или иную сторону под влиянием множества факторов, среди которых могут быть и случайные.

Приведем примеры экономических показателей, основанных на вычислении средней величины и раскрывающих ее сущность:

• расчет средней заработной платы работников предприятия осуществляется делением общего фонда заработной платы на число работников;
• средний размер вклада в банке находят делением суммы вкладов в денежном выражении на количество вкладов;
• для определения средней дневной выработки одного работника необходимо объем работ (количество деталей), выполненных работником за определенный период разделить на число дней в этом периоде.

Виды средних величин, используемых в статистике

Рассмотрим основные виды средних величин, используемых при решении социально-эконмических и аналитических задач.

Средняя арифметическая простая вычисляется по формуле:

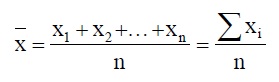Средняя арифметическая простая используется в тех случаях, когда расчет осуществляется по не сгруппированным данным. Пример применения формулы средней арифметической простой представлен в задаче 1.

Средняя арифметическая взвешенная определяется по формуле:

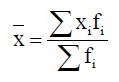При расчете средних величин отдельные значения осредняемого признака могут повторяться, встречаться по несколько раз. В подобных случаях расчет средней производится по сгруппированным данным или вариационным рядам. Пример применения формулы средней арифметической взвешенной представлен в задаче 2.

Средняя гармоническая простая определяется по формуле:

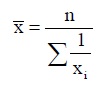Средние гармонические используются тогда, когда по экономическому содержанию имеется информация для числителя, а для знаменателя ее необходимо предварительно определить.

Средняя гармоническая взвешенная определяется по формуле:

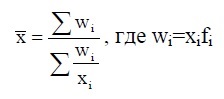Данная формула используется для расчета средних показателей не только в статике, но и в динамике, когда известны индивидуальные значения признака и веса W за ряд временных интервалов. Пример применения формулы средней гармонической взвешенной представлен в задаче 3.

Средняя геометрическая простая (невзвешенная) опеределяется по формуле:

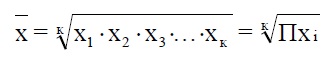Наиболее широкое применение этот вид средней получил в анализе динамики для определения среднего темпа роста.

Средняя квадратическая простая (невзвешенная) опеределяется по формуле:

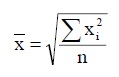Средняя квадратическая лежит в основе вычислений ряда сводных расчетных показателей.

Источник видео: https://www.youtube.com/watch?v=TSAnBo89WGw

Источник конспекта: http://www.ekonomika-st.ru/drugie/metodi/metodi-statistika-1-3.html

Файлы

Нет дополнительных материалов для этого занятия.