Статистика. Статистическое наблюдение.

Комментарии преподавателя

Пусть требуется изучить генеральную совокупность относительно не­которого количественного признака (показателя) X. Извлечем из гене­ральной совокупности выборку. При этом оказалось, что значение случайной величиныX, равное x1, наблюдалось п1 раз, значение х2 - п2 раз, ..., хk - nk раз. Объем выборки - 

Наблюдаемые значения xi есть варианты, а последовательность вариант, записанных в возрастающем порядке, есть вариационный ряд. Числанаблюдений ni, есть частоты, а их отношение к объему выборки 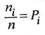- относительные частоты.

Вариационные ряды распределения подразделяются на дискретные и интервальные.

Дискретными называются вариационные ряды, в которых значения признаков, положенных в основу их образования, являются дискретными; и часто выражены целыми числами. Примерами дискретных вариационных рядов являются распределение рабочих по тарифному разряду; рас­пределение отделов по числу работников и т.п.

 

Дискретные ряды распределения строятся по дискретным признакам, которые варьируются в ограниченных пределах.

Дискретный ряд распределения обычно оформляется в виде статисти­ческого распределения выборки.

2. Статистическим распределением выборки называют перечень ва­риант и соответствующих им частот (или относительных частот).

Статистическое распределение выборки можно задать в виде таблицы, в первой графе которой располагаются варианты , а во второй - соот­ветствующие этим вариантам частоты ni, или относительные частоты Pi .

 

Статистическое распределение выборки

 

Варианты хi	x1	x2	x3	…	xi	…	xk
Число наблюдений (частота) ni	n1	n2	n3	…	ni	…	nk
Относительная частота Pi	P1	P2	P3	…	Pi	…	Pk

 

Интервальными называются вариационные ряды, в которых значе­ния признаков, положенных в основу их образования, выражены в определенных пределах (интервалах). Частоты в этом случае относятся, не к отдельным значениям признака, а ко всему интервалу.

Интервальные ряды распределения строятся по непрерывным количе­ственным признакам, а также по дискретным признакам, варьирующим в значительных пределах.

Интервальный ряд можно представить статистическим распределени­ем выборки с указанием интервалов и соответствующих им частот. При этом в качестве частоты интервала принимают сумму частот вариант, по­павших в этот интервал.

При группировке по количественным непрерывным признакам важ­ное значение имеет определение размера интервала.

3. Величина интервала- разность между наибольшим и наименьшим значениями признака в каждой группе, называемыми границами интерва­ла.

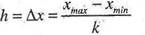Интервалы групп могут быть равными и неравными. Интервалы уста­навливаются в зависимости от характера распределения единиц совокупности по данному признаку. Если вариация (изменение) признака прояв­ляется в сравнительно узких границах и распределение носит более или менее равномерный характер, то целесообразно устанавливать равные ин­тервалы. В этом случае величину интервала определяют по формуле:

где хтах , хт1п - соответственно максимальное и минимальное значения признака в ряду;

к -число интервалов (групп).

Часто строят ряды с равновеликими интервалами. При построении вариационного ряда с равными интервалами определяют число групп (к) и величину интервала (h).

Оптимальное число групп (интервалов) может быть определено по формуле Стерджесса:

K=1+3.322 lg n,

где n - число единиц совокупности.

Сами интервалы могут быть закрытыми(с указанием нижней и верхней границ) и открытыми(с указанием лишь одной из границ интервала).

При количественных группировках следует обращать внимание на правильное обозначение нижней и верхней границ интервала. При образовании интервалов по дискретным признакам это достигается посредством обозначения верхней и нижней границ смежных интервалов значениями признаков, отличных на единицу.

При построении интервальных вариационных рядов по непрерывным признакам необходимо указать, в какой интервал входит значение признака, являющегося границей смежных интервалов. То есть для устранения неопределенности необходимо решить вопрос о том, считать ли верхние границы каждой группы «включительно» или «исключительно».

После того как в результате сводки, материал статистического наблюдения сгруппирован, он, как правило, представляется в виде таблиц.

4. Статистическая таблица- форма наиболее рационального, нагляд­ного и систематического изложения числовых результатов сводки и группировки статистических, материалов в виде ряда строк и столбцов. Основными элементами статистической таблицы являются подлежащее и сказуемое.

Подлежащее статистической таблицы - объекты изучения или пере­чень групп совокупности, характеризуемые цифровыми данными.

Сказуемое статистической таблицы - это цифровые показатели, Ко­торые характеризуют изучаемый объект. Сказуемое таблицы отражает то, что в ней говорится о подлежащем с помощью цифровых данных.

В зависимости от характера построения подлежащего различают про­стые, групповые и комбинационные таблицы.

Простой называется таблица, в подлежащем которой содержится пе­речень объектов наблюдения, например перечень работников предпри­ятия.

Групповойназывается таблица, в подлежащем которой объекты на­блюдения разгруппированы по одному признаку, например по професси­ям работников предприятия. Комбинационнойназывается таблица, в подлежащем которой объекты наблюдения разгруппированы по двум и более признакам в комбина­ции, например, по категориям работников, в том числе и по полу.

По структуре сказуемого различают простые и сложные таблицы.

Простая таблицапредусматривает разработку показателей, характеризующих изучаемые объекты независимо друг от друга.

Сложная таблица предусматривает разработку показателей, характе­ризующих изучаемые объекты в комбинации.

Например, при характеристике объема перевозок в сказуемом табли­цы можно дать перечень признаков, характеризующих объем перевозок по типам тяги и по видам движения. Это будет таблица с простой разработкой сказуемого.

Можно построить таблицу, сказуемое которой будет содержать пере­чень признаков по типам тяги и в том числе по видам движения. Это будет таблица со сложной разработкой сказуемого.

Наряду с таблицами, для наглядного изображения данных наблюде­ния и сводки, в статистике используются графики.

5. Графическим способом изображения статистических данных называют их условное изображение при помощи точек, линий, плоскостей, геометрических фигур и условных знаков. Графики в статистике применяются для: сравнения одноименных показателей, относящихся к различным объектам; наглядного представления структуры совокупности и ее изме­нения; характеристики динамики и степени распространения явления; отображения взаимосвязи явлений.

В зависимости от назначения используют различные виды графиков: линейные, столбиковые, ленточные, секторные, фигурные.

Линейные диаграммыобычно применяют для характеристики ди­намики явлений, их взаимосвязи.

Столбиковые, ленточные диаграммыиспользуются для сравнения значений статистических показателей, характеризующих изучаемые объ­екты в разные моменты времени (за разные периоды времени).

Секторные диаграммыиспользуются для характеристики структуры совокупности.

Фигурные диаграммыиспользуют при сравнении различных явле­ний по степени их распространения.

Дискретные вариационные ряды изображают в виде полигона (много­угольника) распределения.

Полигон распределения строится в прямоугольной системе коорди­нат. На оси абсцисс откладываются варианты, а на оси ординат наносится шкала частот. На оси абсцисс отмечаются точки, соответствующие величинам вариант, и из них восстанавливаются перпендикуляры, длины которых соответствуют частотам конкретных вариант. В результате соедине­ния концов перпендикуляров отрезками прямой, получают полигон рас­пределения. При этом первую точку следует соединить с точкой на оси абсцисс, соответствующей предшествующей варианте, частота которой равна нулю. Последнюю точку следует также соединить с точкой на оси абсцисс, соответствующей варианте, следующей за последней (частота ее также равна нулю). Таким образом получается многоугольник, изображающий распределение признака (рис. 1.1).

 

 

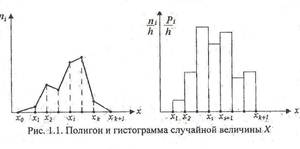
Интервальный ряд графически изображается в виде гистограммы (клеточного графика) распределения.

Гистограмма распределения - ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длины h, а высоты равны отношению ni/h (плотность частоты). В этом слу­чае частота обезличивается и в каждом интервале ее можно отнести к лю­бому значению признака. Площадь i - го прямоугольника равна ni, а пло­щадь гистограммы равна объему выборки п.

Если частоты отнести к серединам интервалов и соединить ординаты прямыми, то получится полигон распределения.

Огива - графическое изображение рядов распределений по накоп­ленным частотам.

В этом случае по оси абсцисс откладывают накопленные частоты (или частости), по оси ординат - значение признака по возрастающей величи­не. Соединяя точки, получают огиву распределения.

Корреляционная таблица - таблица, в которой представлена груп­пировка по двум взаимосвязанным признакам: факторному и результатив­ному. Концентрация частот около диагонали (любой) таблицы свидетель­ствует о наличии связи между признаками.

Источник видео: https://www.youtube.com/watch?v=rpbYIciRzpU

Источник конспекта: http://studopedia.ru/2_87781_graficheskiy-sposob-izobrazheniya-statisticheskih-dannih.html

Файлы

Нет дополнительных материалов для этого занятия.