Теория вероятностей и математическая статистика. Геометрическая вероятность.

Комментарии преподавателя

Не всегда бывает удобно для непосредственного подсчета вероятности использоватьклассическое определение вероятности (например, когда число исходов некоторого опыта бесконечно, как при выборе точки из отрезка и т.п.). Зачастую при этом используется другой метод - геометрический подход к определению вероятности.

Предположим, что случайное испытание можно представить как бросание произвольной точки наудачу в некоторую геометрическую область D (на прямой, плоскости или пространстве, в зависимости от задачи). 
Элементарные исходы – это отдельные точки области D, любое событие – это некоторое подмножество этой области (фактически - пространства элементарных исходов). Можно считать, что все точки D "равноправны", и тогда вероятность попадания точки в некоторое подмножество этой области пропорциональна мере (длине, площади, объему) подмножества и не зависит от его расположения внутри области и формы. Таким образом приходим к геометрическому определению вероятности.

Геометрическая вероятность некоторого события А определяется формулой: 

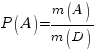
Здесь  – геометрические меры (длины, площади или объемы) всего пространства элементарных исходов и множества исходов, благоприятствующих осуществлению события А.

 В квадрат с вершинами 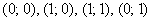  наудачу брошена точка 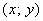. Найдите вероятность того, что координаты этой точки удовлетворяют неравенству.

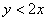Решение: изобразим на чертеже искомый квадрат и прямую :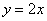 

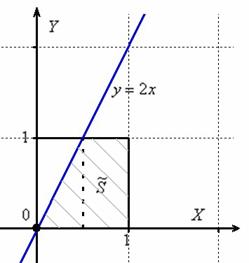
Общему множеству исходов соответствует площадь квадрата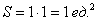 

Прямая 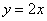 делит квадрат на треугольник и трапецию. Как определить фигуру, которая удовлетворяет условию 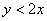? Вспоминаем линейные неравенства: нужно взять любую точку, не принадлежащую прямой 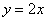, например, точку  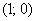и подставить её координаты в неравенство:

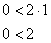
Получено верное неравенство, значит, множеству благоприятствующих исходов соответствует площадь 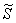 трапеции. Рассчитаем данную площадь как сумму площадей прямоугольного треугольника и прямоугольника:

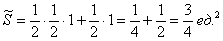
По геометриче­скому определению:
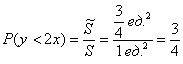 – вероятность того, что координаты брошенной в данный квадрат точки удовлетворяют неравенству.

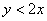Ответ: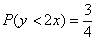 

Задача 

Загадываются два числа 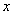 и 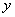 в промежутке от 0 до 5. Какова вероятность, что ? 

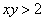Схема решения уже знакома: коль скоро загадываются 2 произвольных числа от нуля до пяти (они могут быть и иррациональными), то общему количеству исходов соответствует площадь квадрата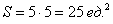  

Изобразим ветвь гиперболы 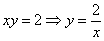, которая делит квадрат на две части:

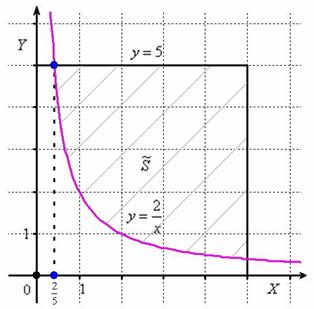
Теперь выясним, какой из этих двух «кусков» удовлетворяет неравенству 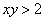. Для этого выберем любую точку, не принадлежащую гиперболе, проще всего взять 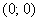, и подставим её координаты в наше неравенство:

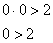
Получено неверное неравенство, а значит, условию 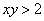 соответствует «верхний кусок», площадь  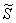 которого вычислим с помощью определённого интеграла.

Уточним нижний предел интегрирования аналитически (найдём точку пересечения гиперболы 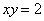 и прямой ):

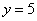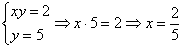
На отрезке  прямая 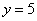 расположена не ниже гиперболы , 
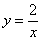по соответствующей формуле:

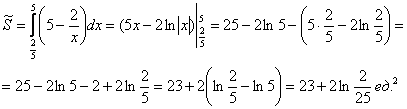
По геометрическому определению:
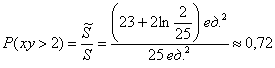 – вероятность того, что произведение двух загаданных в промежутке от 0 до 5 чисел окажется больше двух.

Ответ: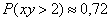 

Задача 

Загадываются два числа 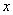 и 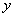 в промежутке от 0 до 10. Какова вероятность, что ? 

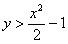Данная задача (как, собственно, и предыдущая) допускает несколько способов расчёта 

 Решение: выполним чертёж:

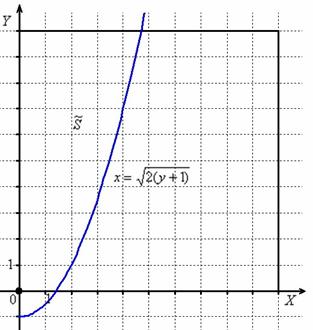
Общее число исходов выражается площадью квадрата 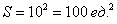. Неравенству  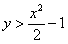соответствует площадь 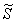, которую вычислим с помощью определённого интеграла, интегрируя по «игрек» (данный метод рассмотрен в статье Объем тела вращения).
Выразим обратную функцию: .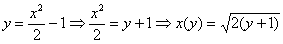
На отрезке 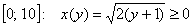, поэтому:

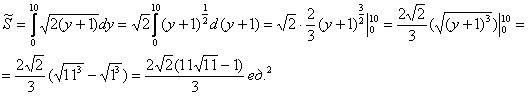
По геометрическому определению:
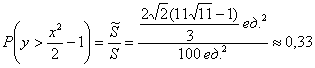 – вероятность того, что два загаданных от нуля до 10-ти числа будут удовлетворять неравенству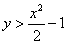 
Ответ: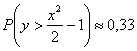 

Источник видео: https://www.youtube.com/watch?v=0dVxlmWsVsg

Источник конспекта: http://www.mathprofi.ru/geometricheskoe_opredelenie_verojatnosti.html

Файлы

Нет дополнительных материалов для этого занятия.