|
Специализация
|
Выполнена Нужна помощь
ПОМОГИТЕ ПОЖАЛУСТА С ГЕОМЕТРИЕЙ!)
МОЖНО БЕЗ РЕШИНИЯ
ЗАДАНИЕ 1
Даны векторы a(вектор) (-6;1;-8) и b вектор (3;2;-2).
Определи, какой угол образован этими векторами.
- Тупой угол
- Острый угол
- Прямой угол
ЗАДАНИЕ 2
Даны векторы a вектор {-3;0;4} и b вектор{1;2;2}.
Определи значение косинуса угла между этими векторами.
(Дробь в ответе не сокращай!).
Ответ: cos(a b(вектрры) )ˆ=
ЗАДАНИЕ 3
Определи угол между векторами, расположенными в кубе.

1. (BB1→DD1→)ˆ= °
2. (D1B1→BD→)ˆ= °
3. (AC→BC−→)ˆ= °
4. (DA→B1D1→)ˆ=
ЗАДАНИЕ 4
Определи косинус ∡L треугольника ALC, если даны координаты вершин треугольника:
A(1;3;2)
L(1;0;-2)
C(-1;-2;-3)
(запиши ответ в виде не сокращённой дроби).
Ответ: cos∡L=
- Геометрия
- Курсовик
- Сдать до 03.10.2018 22:00
Выполнена Нужна помощь
Пожалуйста, помогите с геометрией
можно без решения
Задание 1.

\ А\ - МОДУЛЬ А
|вектор a |=8 |вектор b | =10 угол α=150°
Определи скалярное произведение данных векторов.
(Если в ответе нет корня, под знаком корня пиши 1)
Ответ :____
ЗАДАНИЕ 2
Определи скалярное произведение векторов a (вектор) {4;8;-6} и b(вектор) {-7;1;7}.
Ответ: a и b =
ЗАДАНИЕ 3
Даны векторы a вектор(-8;7;-5) и b вектор(1;x;-6).
Найди значение x, если a b (векторы)=50.
Ответ: x=
ЗАДАНИЕ 4
Даны векторы
a(вектор) {-4;-2;1}; b(вектор) {0;1;2}; c(вектор) {3;-3;9}.
Которые из них образуют прямой угол?
a и b(векторы)
- Неизвестно
- Нет
- Да
b и c(векторы)
- Нет
- Неизвестно
- Да
a и c (векторы)
- Неизвестно
- Да
- Нет
ЗАДАНИЕ 5
Определи неизвестную координату, если данные векторы перпендикулярны.
(Если значений переменной несколько, введи их в поле для ответа в порядке возрастания без пустых мест через точку с запятой).
1. Даны векторы a→{6;2;-8} и b→{6;k;6}.
k=
2. Даны векторы n→{a;2;-8} и m−→{a;a;6}.
a=
- Геометрия
- Курсовик
- Сдать до 03.10.2018 22:00
Выполнена Нужна помощь
Выполнена Нужна помощь
Решение не нужно))
Задание 1.
Сторона равностороннего треугольника равна 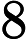
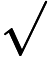
 дм
дм
Вычисли:
1. Площадь треугольника;
2. Радиус окружности, вписанной в треугольник;
3. Радиус окружности, описанной около треугольника.
1. 
 _________
_________
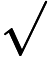 дм
дм 2.
2. 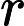 =________дм 3.
=________дм 3. 
 __________дм
__________дм
ЗАДАНИЕ 2
Определи число сторон выпуклого правильного многоугольника или сделай вывод, что такой многоугольник не существует, если дана сумма всех внутренних углов (если многоугольник не существует, то вместо числа сторон пиши 0):
1. Если сумма углов равна 610, то многоугольник не существуетсуществует______, число сторон — .
2. Если сумма углов равна 540, то многоугольник не существуетсуществует______, число сторон —
ЗАДАНИЕ 3

Определи величину одного внутреннего угла правильного выпуклого 20- угольника:
Ответ (Если это необходимо, округли ответ до целых): _____°
ЗАДАНИЕ 4
Дан равносторонний треугольник. Вычисли неизвестные величины, если BO=6м

r — радиус вписанной окружности
r =___ м
OD=___м
BE=___м
AD=___м
EC=
- 3√3
- 3√2
- 6√2
- 6√3
ЗАДАНИЕ 5

O — центр окружности, радиус MO=11 см.
Площадь полукруга равна ___π см2
ЗАДАНИЕ 6
Чтобы обойти поле в форме круга на скорости 4 км/ч, необходимо времени на 45минут больше, чем времени, чтобы перейти прямо по диаметру.
Вычисли приближенную длину круговой дороги вокруг поля, используй значение π≈3,14.
(Округли свои расчёты до десятых).
ина дороги приблизительно равна ____километрам.
ЗАДАНИЕ 7
Вычисли радиус круга, если его площадь S=64πм^2
R=____ м
ЗАДАНИЕ 8
Вырази из формулы длины окружности C=2πR
число2=
ЗАДАНИЕ 9
У прямой четырёхугольной призмы в основании лежит ромб с углом 60° и стороной 7 см. Определи площадь большего диагонального сечения, если высота призмы — 7 см.
Ответ: площадь большего диагонального сечения равна ____√____см2
ЗАДАНИЕ 10
Сколько граней и рёбер имеют данные многогранники?
1. У призмы 10-угольника___ граней и ____ рёбер.
2. У пирамиды 7-угольника__ граней и___ рёбер
ЗАДАНИЕ 11
Дана правильная 6-угольная пирамида со стороной основания 32 см и апофемой 8 см.
Определи боковую поверхность пирамиды.
Ответ: Sбок.=___см2
ЗАДАНИЕ 12
Известно, что измерения прямоугольного параллелепипеда равны 12 см, 18 см и 8 см.
Скольким см должно быть ребро куба с таким же объёмом, как у данного прямоугольного параллелепипеда?
Ответ: длина ребра куба равна ___см.
- Геометрия
- Домашнее задание
- Сдать до 12.04.2018 21:49
Выполнена Нужна помощь
Решите пожалуйста 3 задачи по геометрии (решение и рисунок очень нужны)
ЗАДАЧА 1
DABC - правильная пирамида
AB=BC=AC=5 см
DO- высота
DO= корень из 13
Найти : Sбок.
ЗАДАЧА 2
ABCDA1B1C1D1- прям. призма
ABCD - ромб
угол A=60 градусов
AA1=10
Sбок =240 см^2
Найти: S(BB1D1D)
ЗАДАЧА 3
Дано:
DABC - пирамида
треуг. АВС- прямоуг.
угол С=90 градусов
угол В=30 градусов
DO- высота
DO=4 cm
угол ADO= угол BDO = угол СDO
Найти : Sбок
- Геометрия
- Домашнее задание
- Сдать до 06.04.2018 18:33
Выполнена Нужна помощь
Выполнена Нужна помощь
ХИМИЯ!
НАЗВАНИЕ ОПЫТА: взаимодействие карбоновых кислот с солями слабых неорганических кислот
ДЕЙСТВИЯ: в пробирку налить 1мл карбоната натрия и по каплям добавить уксусную кислоту
Какие наблюдения и вывод можно сделать??
УРАВНЕНИЯ ХИМ.РЕАКЦИЙ:
Запишите УХР в молекулярном, ионном и сокращенном ионном виде
- Химия
- Домашнее задание
- Сдать до 06.03.2018 17:37
Выполнена Нужна помощь
НАЗВАНИЕ ОПЫТА:
Взаимодействие карбоновых кислот с основаниями.
ДЕЙСТВИЯ
налить в пробирку раствор гидроксида натрия,добавить 1 каплю фенолфталеина. Затем добавить к содержимому пробирки уксусную кислоту
УРАВНЕНИЕ ХИМИЧЕСКИХ РЕАКЦИЙ
Запишите УХР, назовите продукты
- Химия
- Домашнее задание
- Сдать до 06.03.2018 17:28
Выполнена Нужна помощь
Выполнена Нужна помощь
МОЖНО БЕЗ РЕШЕНИЯ))
ЗАДАНИЕ 7
Вычисли значение выражения
4cos^2 460°+4sin^2 620°
ЗАДАНИЕ 8
Вычисли:
sin42°⋅cos12°−cos42°⋅sin12°
Ответ:
- cos30°=3√2
- sin30°=1/2
- cos60°=1/2
- sin45°=2√2
ЗАДАНИЕ 9
Найди значение выражения:
cos107°⋅cos17°+sin107°⋅sin17°
Ответ:
- sin45°=2√2
- sin90°=1
- cos90°=0
- cos60°=1/2
ЗАДАНИЕ 10
1. Упрости данное выражение:
cos38°⋅cos22°−sin38°⋅sin22°
Отметь полученный после упрощения результат:
- sin60°
- cos30°
- sin45°
- cos60°
2. Определи значение полученного выражения и отметь его среди представленных вариантов.
Ответ:
- 2√2
- 3√2
- 1/2
- 1
ЗАДАНИЕ 11
Укажи все равенства, которые являются записью формул синуса (косинуса) суммы или разности аргументов
- cos(α−β)=cosα⋅cosβ+sinα⋅sinβ
- cos(α+β)=cosα⋅sinβ−sinα⋅cosβ
- cos(α−β)=cosα−cosβ
- sin(α+β)=cosα⋅sinβ+sinα⋅cosβ
- sin(α+β)=sinα⋅cosβ+cosα⋅sinβ
- sin(α+β)=sinα+sinβ
ЗАДАНИЕ 12
Приведи выражение к упрощенному виду
cos(α-β)−cosα⋅cosβ
Выбери правильный ответ из предложенных вариантов
- cosα⋅cosβ
- sinα⋅cosβ
- cosα⋅sinβ
- sinα⋅sinβ
ЗАДАНИЕ 13
Вычисли:
1) cos40°⋅cos5°−sin40°⋅sin5°
2) sin55°⋅cos5°+cos55°⋅sin5°
- 1)2√2,2)2√2
- 1)2√2,2)3√2
- 1)1.2,2)3√2
- 1)3√2,2)1.2
ЗАДАНИЕ 14
Упрости выражение:
sin32°⋅cos14°+cos32°⋅sin14° =
ЗАДАНИЕ 15
Найди значение выражения:
sin8π/15⋅cos7π/10−cos8π/15⋅sin7π/10
Ответ выбери из приведенных вариантов решений:
- 1/2
- 3√2
- 2√2
- −1/2
- Алгебра
- Домашнее задание
- Сдать до 05.03.2018 21:11
-
Вы можете создать новое задание прямо отсюда. Удобно, правда?
-
Здесь можно найти все задания созданные вами за всё время
-
Здесь вы найдете все задание для которых вы назначены исполнителем.
-
Вы можете отфильтровать задания по их статусу для более вдумчивого изучения ситуации.
























































